Project-Euler-700 Eulercoin

Posted on Edited on In

D_1

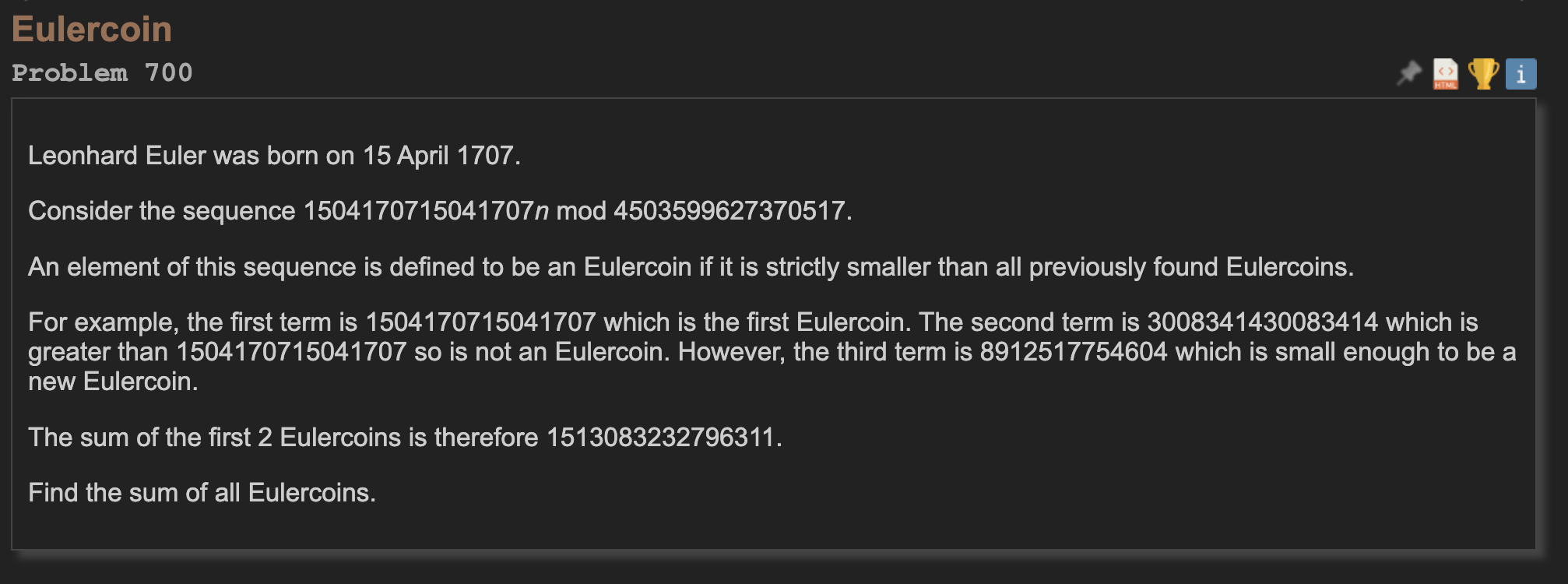
$$
EulerCoin_n = (1504170715041707 * n) mod (4503599627370517)
$$

We can see finally the $ EulerCoin_n $ will become 1 and then the $n$ should be $3451657199285664$, the reason is below:

From $pow(1504170715041707,-1,4503599627370517) = 3451657199285664$,

so we have $1504170715041707 * 3451657199285664 \ mod \ 4503599627370517 = 1$

Now we know the upper limit of $n$ is $3451657199285664$, that is still too big. Hmm, it will cost us 1 year to calculate the result.

If we go straight, we can get the first 15 results of $n$ and $EulerCoin$ very easily:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
n = 3, EulerCoin_n = 8912517754604
n = 506, EulerCoin_n = 2044785486369
n = 2527, EulerCoin_n = 1311409677241
n = 4548, EulerCoin_n = 578033868113
n = 11117, EulerCoin_n = 422691927098
n = 17686, EulerCoin_n = 267349986083
n = 24255, EulerCoin_n = 112008045068
n = 55079, EulerCoin_n = 68674149121
n = 85903, EulerCoin_n = 25340253174
n = 202630, EulerCoin_n = 7346610401
n = 724617, EulerCoin_n = 4046188430
n = 1246604, EulerCoin_n = 745766459
n = 6755007, EulerCoin_n = 428410324
n = 12263410, EulerCoin_n = 111054189
n = 42298633, EulerCoin_n = 15806432

We find then the upper limit of $EulerCoin_n$ is only $15806432$. If we go reverse direction, we know $EulerCoin_n$, could we get the corresponding value of $n$ and check if $n$ is decreasing? The answer is we can:

$$EulerCoin_n = (1504170715041707 * n) mod (4503599627370517) $$
$$ => (EulerCoin_n * 3451657199285664) mod 4503599627370517 = n$$

1
2
3
4
5
6
before = 3451657199285664
for EulerCoin_n in range(1, 15806432):
    res = 3451657199285664*EulerCoin_n%4503599627370517
    if(res < before):
        before = res
        sumt += EulerCoin_n

Plus the first 15 results of $EulerCoin_n$, we can get the final sum.