AtCoder Grand Contest 004
A Divide a Cuboid
题意是给出一个A*B*C的立方体,以一个面来切分成两部分,要求这两部分体积之差最小。
如果A、B、C有一个是偶数,那么直接就是0。都是奇数的话,从A*B、B*C、A*C里面选一个最小的。
B Colorful Slimes
题意是有N种颜色,有两种方法得到第i种颜色。
1.直接花费Ai秒得到第i种颜色。
2.念一个咒语,花费k秒的时间,使得已经得到的第i种颜色变成第i+1种颜色,第N种颜色变成第1种颜色。
枚举所要用到的咒语数量,当使用x次咒语时,对于第i种颜色来说,得到的代价就是前面x个颜色的最小值。
C AND Grid
题意是有两个h*w的格子A和B,图上每个格子不是黑点就是白点,A和B都是联通的图,现在A和B相交到一起形成图C,每个方格做与运算。给出了两个相交的图C,求原来的两个图A和B,已知图C的黑点一定不在边界上。
会发现这样联通的情况。。。
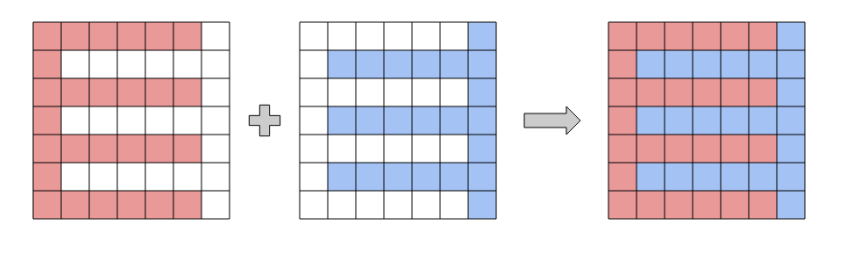
之后根据图C,就可以这样构造图A和图B。
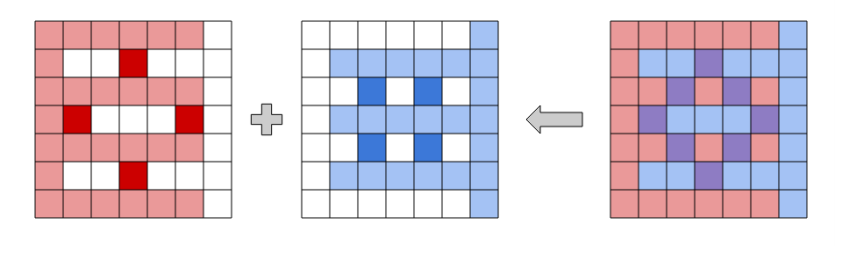
D Teleporter
题意是给出一个有向图,任意一个点都可以到达点1,要求改变图中一些边的终点,使得所有点准确经过k次之后到达点1。
经过k次而不是经过小于等于k次到达点1,可以分析出这样点1的那个出边一定是指向点1的。不是的话,就要修改。
这样,所有的点就要到点1的距离小于等于k就可以了。
贪心。以1为根节点深搜,当一个节点其子节点的最大深度大于等于k的时候,这条边就需要被剪掉,连到1节点。(一开始想判断一个点当期深度大于k的时候就需要剪掉,后来发现需要计算距离,下面可能有还需要剪掉的点,这种做法就比较麻烦了)
E Salvage Robots
题意是在h*w的格子上,有一个出口,所有的机器人遵循相同的指令方向,当机器人出界的时候,在机器人作废。问最终最多能有多少个机器人达到出口。
这个题我想了很久很久很久很久。。。一直没有看懂题解的意思。。。
后来在问了LYC之后,终于。。。
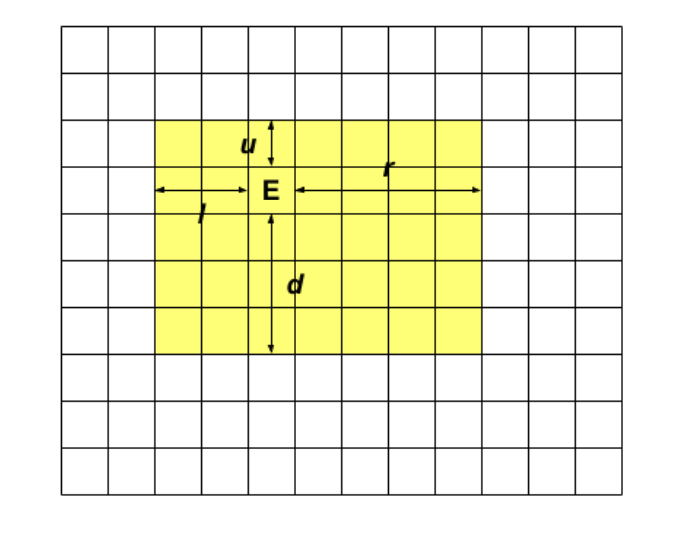
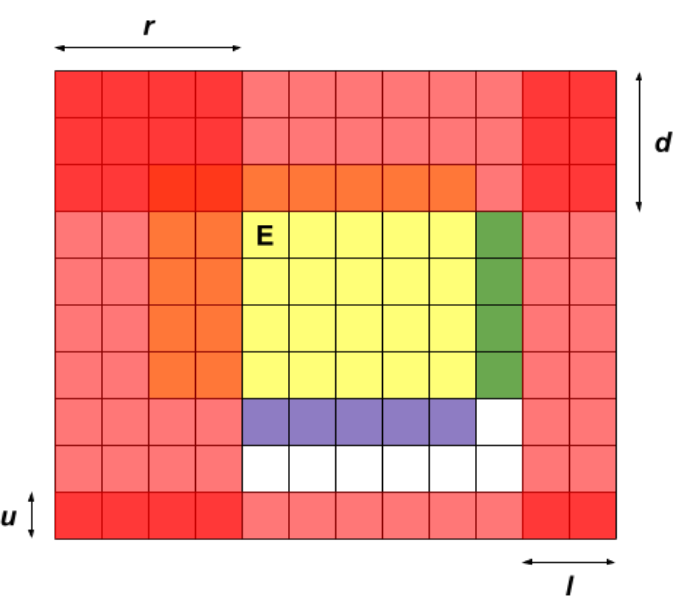
首先肯定不能考虑这些机器人动,考虑出口动,然后记录出口向四个方向的移动距离。上面的图就表示出口向上走了u步,向下走了d步,向左走了le步,向右走了ri步,黄色区域就代表救到的机器人,那么此时会发现,假设出口往上走了u步的话,下面的u行机器人就不能救了,所以下图中红色区域的机器人就代表要么是之前已经救过的,要么就是已经爆炸的。白色框里的就代表没有确定的,还待解决的。
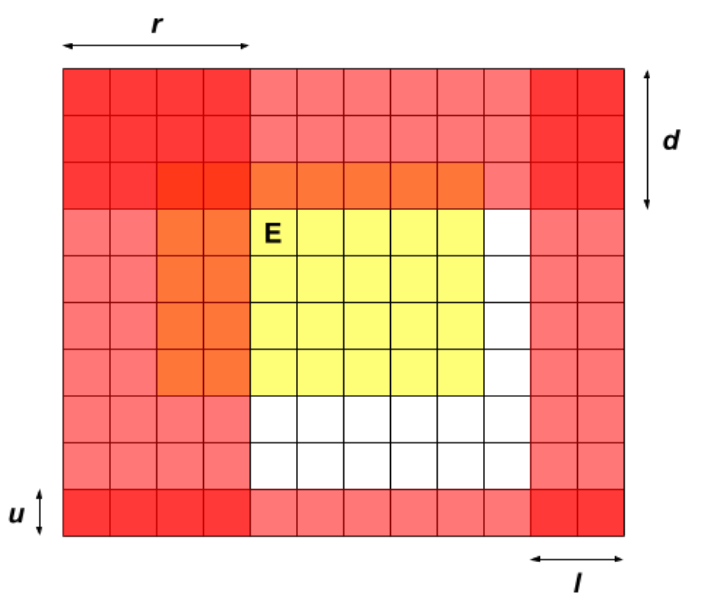
所以搞到现在,大致思路就有了。用dp[le][ri][u][d]来表示当前状态,考虑四个方向,假设当前机器人往右走,那么就可以得到下图中绿色框里的机器人,向下走就可以得到紫色框里的机器人。
F Namori
题意是n个点m(n-1<=m<=n)条边的无向联通图,一开始所有点都是白色,每次操作选择两个相邻的点,翻转它们的颜色,要求最终都是黑点,求最少的操作次数。
先考虑m=n-1的情况,这个题目再一次神奇的转化了。。。
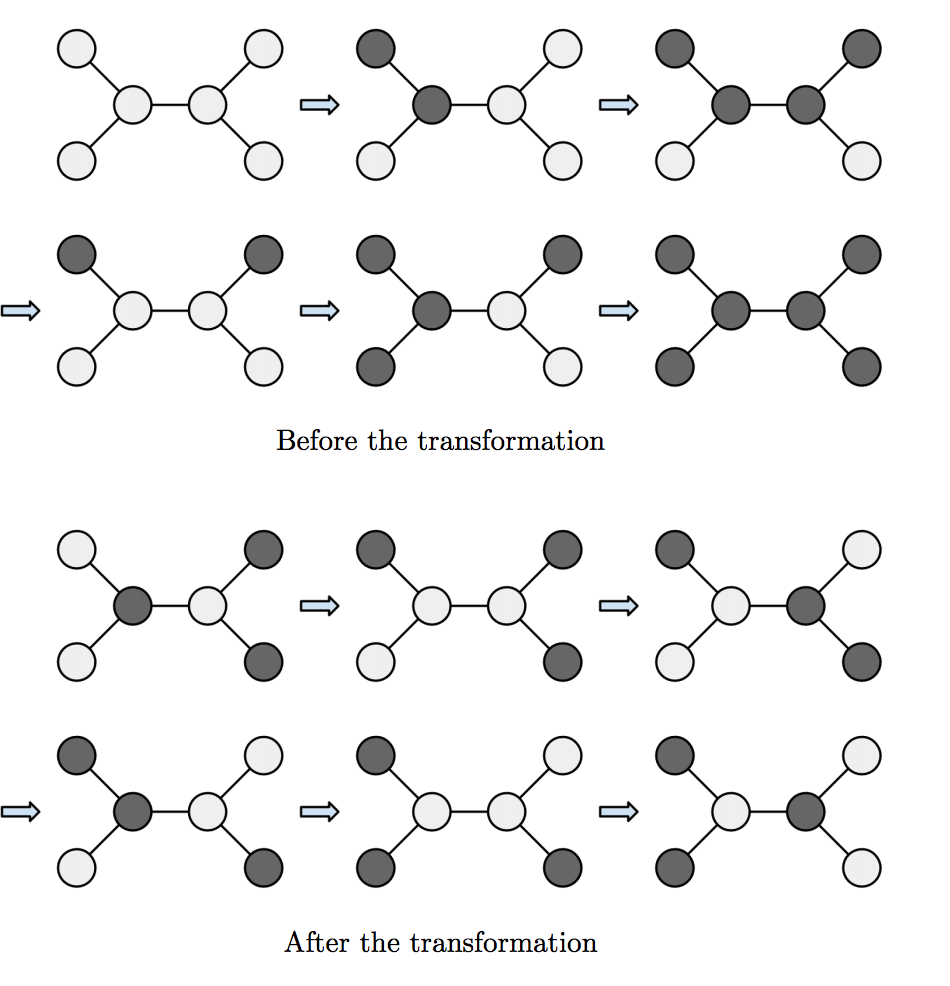
因为树是一个二分的图,把树节点二分染色之后,每次操作相当于把黑色通过这个边转移到了白色节点上,那么我就记录每一条边都运输了多少黑色,也就是题解中所说的token。如果能把问题转换到这里,这个1500分倒还真是好拿啊。。。
之后就是考虑环的情况了,因为最多n条边,所以考虑把环上的边拿掉会是一个什么情况。
偶数环:判断剩下的图依旧得是二分图,三分这条边上经过的token数+其余边经过的token数,取最小值。
奇数环,此时这两个点要么就是都带token,要么就是都不带token。把其余的多的或者少的token分配到这两个点上,再算一遍整个图。