上周末做了rng_58 办的AtCoder Grand Contest 001 ,英文题解在这里 。比赛的时候只做出了两道题,第二题还一直wa,导致第三题没时间了,博主比较弱。。。。后来自己慢慢补题,发现D E F都是很神的题。。。在这里记一下总结吧。
A BBQ Easy 题意是给出2*n个长度,每两个在一起,这两个的长度算两个中短的那个,之后算总的最大长度。
直接排序,把奇数位的加起来就是总的最大长度。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 #include <iostream> #include <functional> #include <algorithm> #include <cstring> #include <vector> #include <string> #include <cstdio> #include <cmath> #include <queue> #include <stack> #include <deque> #include <list> #include <set> #include <map> using namespace std;typedef long long ll;#define eps 1e-10 #define LL_INF 0x33ffffffffffffff #define INF 0x3f3f3f3f #define mem(a, b) memset(a, b, sizeof(a)) #define sa(n) scanf("%d" , &(n)) #define mp make_pair #define ff first #define ss second #define pb push_back const int maxn = 405 ;const ll mod = 1000000007 ;const double PI = acos (-1.0 ); int n;int val[maxn]; void solve () int res = 0 ; int i, j, k; for (i = 1 ;i <= 2 *n; i++) { sa (val[i]); } sort (val + 1 , val + 2 *n + 1 ); for (i = 1 ; i <= 2 * n - 1 ; i = i + 2 ) { res += val[i]; } printf ("%d\n" , res); } int main () while (scanf ("%d" , &n) != EOF) { solve (); } return 0 ; }
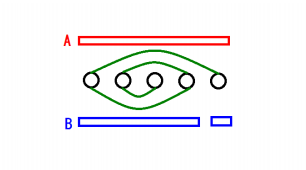
B Mysterious Light B题比较好玩,等边三角形,长度为n,一束光从位置x处发出,遇到边会发生反射,遇到自己的路径也会发生反射,问这束光走过的路程。
会发现这束光就是在一个平行四边形里面走,而且这个平行四边形越走越小,越走越小。边长设为a,b(a>b),之后如果继续走的话,平行四边形就变为b,a%b。于是乎,写一个递归算当前平行四边形走过的路程。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 #include <iostream> #include <functional> #include <algorithm> #include <cstring> #include <vector> #include <string> #include <cstdio> #include <cmath> #include <queue> #include <stack> #include <deque> #include <list> #include <set> #include <map> using namespace std;typedef long long ll;#define eps 1e-10 #define LL_INF 0x33ffffffffffffff #define INF 0x3f3f3f3f #define mem(a, b) memset(a, b, sizeof(a)) #define sa(n) scanf("%d" , &(n)) #define mp make_pair #define ff first #define ss second #define pb push_back const int maxn = 405 ;const ll mod = 1000000007 ;const double PI = acos (-1.0 ); ll n, x; ll cal (ll n, ll x) if (x <= 0 ) { return 3 * n; } if (n % x == 0 ) { return n * 3LL ; } else { return n / x*x * 3LL + cal (x, n%x); } } void solve () ll res = 0 ; if (x * 2LL >= n) { res = cal (x, n - x); } else { res = cal (n - x, x); } printf ("%lld\n" , res); } int main () while (cin >> n >> x) { solve (); } return 0 ; }
C Shorten Diameter 题意是给出一棵树,要求树中最长的路径为k,问要达到要求的话,至少要删除多少个点。
n一共才1000,直接分k是奇数还是偶数来爆搜,k如果是奇数,那么按照边来爆搜,每个点最多(k-1)/2个。如果k是偶数,那么按照点来搜,每个方向最多k/2个。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 #include <iostream> #include <functional> #include <algorithm> #include <cstring> #include <vector> #include <string> #include <cstdio> #include <cmath> #include <queue> #include <stack> #include <deque> #include <list> #include <set> #include <map> using namespace std;typedef long long ll;#define eps 1e-10 #define LL_INF 0x33ffffffffffffff #define INF 0x3f3f3f3f #define mem(a, b) memset(a, b, sizeof(a)) #define sa(n) scanf("%d" , &(n)) #define mp make_pair #define ff first #define ss second #define pb push_back const int maxn = 500005 ;const ll mod = 998244353 ;const double PI = acos (-1.0 ); int n, k;vector<int >edge[maxn]; int u[maxn], v[maxn]; int dfs (int x, int fa, int dis) int res = (dis<0 ); int sz = edge[x].size (); int k = 0 ; int i,j; for (i=0 ;i<sz;i++) { k = edge[x][i]; if (k == fa)continue ; res += dfs (k, x, dis - 1 ); } return res; } void solve () sa (n), sa (k); int i, j; for (i=1 ;i<=n-1 ;i++) { sa (u[i]), sa (v[i]); edge[u[i]].push_back (v[i]); edge[v[i]].push_back (u[i]); } int res = n; if ((k & 1 ) == 0 ) { for (i=1 ;i<=n;i++) { res = min (res, dfs (i, -1 , k / 2 )); } } else { for (i=1 ;i<=n-1 ;i++) { res = min (res, dfs (u[i], v[i], (k - 1 ) / 2 ) + dfs (v[i], u[i], (k - 1 ) / 2 )); } } printf ("%d\n" , res); } int main () solve (); return 0 ; }
D Arrays and Palindrome 题意很拗口,有两个数组a和b,a数组元素的和与b数组元素的和都是n。
有一个字符串长度为n,如果满足了下面(1)(2)的条件,那么能推出第三个条件:
(1)起始的a1个字符,接下来的a2个字符,接下来的a3个字符。。。。都是回文串。
(2)起始的b1个字符,接下来的b2个字符,接下来的b3个字符。。。。都是回文串。
(3)这个字符串的每一个字符都是相等的。
然后给出a数组的一个排列,需要你去求a数组,和b数组。
这个题于我而言很神了。。。
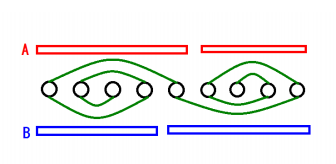
可以发现当a数组只有一个元素{x}的时候,那么b数组{x-1,1}就可以满足条件。
然后与此类似,两个数的时候{x,y}变成{x-1,y+1}就能够满足题目要求。
做到这里我的感觉就是当这个块为奇数的时候,那么中间的那个点是没有连接的,所以当奇数块多的时候,应该就不行了,多到多少呢?如果奇数块的个数超过两个,就达不到题目要求了。
证明:假设a有X个奇数元素,字符串长度为N,那么连接两点的边的个数为(N-X)/2, b有Y个奇数元素,连接两点边的个数为(N-Y)/2,然后因为要互相都等于,所以边数至少要N-1个,就有(N-X)/2 + (N-Y)/2 >= N-1推出X+Y<=2,可知a最多有两个奇数元素,才能符合题目要求,否则直接输出。
这样剩下的情况就是加1减1了,2个奇数的话,放两边。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 #include <iostream> #include <functional> #include <algorithm> #include <cstring> #include <vector> #include <string> #include <cstdio> #include <cmath> #include <queue> #include <stack> #include <deque> #include <ctime> #include <list> #include <set> #include <map> using namespace std; typedef long long ll;#define eps 1e-10 #define LL_INF 0x3fffffffffffffff #define INF 0x3f3f3f3f #define mem(a, b) memset(a, b, sizeof(a)) #define sa(n) scanf("%d" , &(n)) #define mp make_pair #define ff first #define ss second #define pb push_back const int maxn = 1e5 + 5 ;const ll mod = 998244353 ;const double PI = acos (-1.0 ); int n, m;int val[maxn]; void solve () int i, j, k; sa (n), sa (m); vector<int >odd; vector<int >even; for (i=1 ;i<=m;i++) { sa (val[i]); if (val[i] & 1 ) { odd.push_back (val[i]); } else { even.push_back (val[i]); } } if (n == 1 ) { printf ("1\n" ); printf ("1\n" ); printf ("1\n" ); } else { int od_sz = odd.size (); int ev_sz = even.size (); if (od_sz > 2 ) { puts ("Impossible" ); } else { if (od_sz == 0 ) { for (i=0 ;i<ev_sz-1 ;i++) { printf ("%d " , even[i]); } printf ("%d\n" , even[ev_sz - 1 ]); printf ("%d\n" , ev_sz + 1 ); printf ("1 " ); for (i=0 ;i<ev_sz-1 ;i++) { printf ("%d " , even[i]); } printf ("%d\n" , even[ev_sz - 1 ] - 1 ); } else if (od_sz == 1 ) { if (ev_sz == 0 ) { printf ("%d\n" , odd[0 ]); printf ("2\n" ); printf ("%d %d\n" , odd[0 ] - 1 , 1 ); } else { printf ("%d " , odd[0 ]); for (i=0 ;i<ev_sz-1 ;i++) { printf ("%d " , even[i]); } printf ("%d\n" , even[ev_sz - 1 ]); printf ("%d\n" , m); printf ("%d " , odd[0 ] + 1 ); for (i=0 ;i<ev_sz-1 ;i++) { printf ("%d " , even[i]); } printf ("%d\n" , even[ev_sz - 1 ] - 1 ); } } else if (od_sz == 2 ) { if (ev_sz == 0 ) { if (odd[0 ] == 1 && odd[1 ] == 1 ) { printf ("1 1\n" ); printf ("1\n" ); printf ("2\n" ); } else { sort (odd.begin (), odd.end ()); printf ("%d %d\n" , odd[0 ], odd[1 ]); printf ("2\n" ); printf ("%d %d\n" , odd[0 ] + 1 , odd[1 ] - 1 ); } } else { printf ("%d " , odd[0 ]); for (i=0 ;i<ev_sz;i++) { printf ("%d " , even[i]); } printf ("%d\n" , odd[1 ]); vector<int >r; r.push_back (odd[0 ] + 1 ); for (i=0 ;i<ev_sz;i++) { r.push_back (even[i]); } if (odd[1 ] - 1 ) { r.push_back (odd[1 ] - 1 ); } printf ("%d\n" , r.size ()); int sz = r.size (); for (i=0 ;i<sz;i++) { if (i == sz-1 ) { printf ("%d\n" , r[i]); } else { printf ("%d " , r[i]); } } } } } } } int main () solve (); return 0 ; }
E BBQ Hard 题意是给出N个pack,每一个pack有A个beef,B个pepper。从N个里面挑两个pack放在一起,问一共有多少种摆放方法。假设取出来的是Ai+Aj,Bi+Bj,那么只这一份的摆放种类为:
$$\frac{(A{i}+A{j}+B{i}+B{j})!}{(A{i}+A{j})!*(B{i}+B_{j})!}$$
然后这时候假设这个函数为f(x,y),即有:
$$f(x,y)=\frac{(x+y)!}{x!*y!}$$
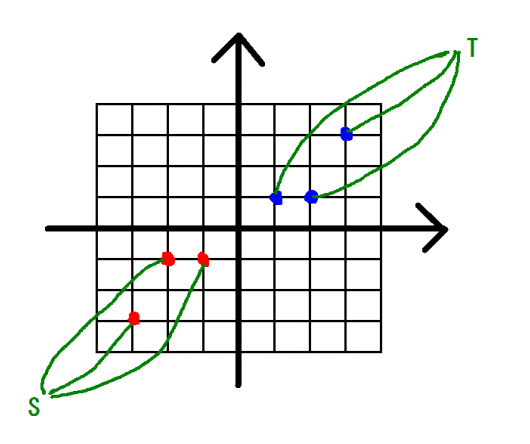
于是乎发现一件事情,这个函数就等于走方格的数量。
即从坐标(0,0)走到坐标(x,y)只能向上或者向右走的话有多少种走法。那对于f(Ai+Aj,Bi+Bj)来说,即是从坐标(0,0)走到坐标(Ai+Aj,Bi+Bj),也就是(-Ai,-Bi)走到(Aj,Bj)。然后这样的话就可以dp来求了。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 #include <iostream> #include <functional> #include <algorithm> #include <cstring> #include <vector> #include <string> #include <cstdio> #include <cmath> #include <queue> #include <stack> #include <deque> #include <ctime> #include <list> #include <set> #include <map> using namespace std;typedef long long ll;typedef pair<int , ll> pill; #define eps 1e-10 #define LL_INF 0x3fffffffffffffff #define INF 0x3f3f3f3f #define mem(a, b) memset(a, b, sizeof(a)) #define sa(n) scanf("%d" , &(n)) #define mp make_pair #define ff first #define ss second #define pb push_back const int maxn = 4e3 + 5 ;const ll mod = 1e9 +7 ;const double PI = acos (-1.0 ); int n;int u[200005 ],v[200005 ];ll fac[2 *maxn],infac[2 *maxn]; ll cnt[maxn][maxn]; ll po (ll x,ll y) ll res=1 ; while (y) { if (y&1 ) { res =(res*x)%mod; } x=x*x%mod; y=y>>1 ; } return res; } void init () int i,j,k; fac[0 ]=1 ; for (i=1 ;i<=8000 ;i++) { fac[i]=(fac[i-1 ]*i)%mod; infac[i]=po (fac[i],mod-2 ); } } ll cal (int x,int y) return ((fac[x+y]*infac[x])%mod*infac[y])%mod; } void solve () int i,j,k; memset (cnt,0 ,sizeof (cnt)); for (i=1 ;i<=n;i++) { sa (u[i]),sa (v[i]); cnt[2000 -u[i]][2000 -v[i]]++; } for (i=0 ;i<=4000 ;i++) { for (j=0 ;j<=4000 ;j++) { if (i>0 ) { cnt[i][j] = (cnt[i][j]+cnt[i-1 ][j])%mod; } if (j>0 ) { cnt[i][j] = (cnt[i][j]+cnt[i][j-1 ])%mod; } } } ll r=0 ; for (i=1 ;i<=n;i++) { r = (r+cnt[2000 +u[i]][2000 +v[i]])%mod; r = ((r-cal (2 *u[i],2 *v[i]))%mod+mod)%mod; } r = (r*po (2 ,mod-2 ))%mod; printf ("%lld\n" ,r); } int main () init (); while (scanf ("%d" ,&n)!=EOF) { solve (); } return 0 ; }
F Wide Swap F题题意是给出了一个1到n的排列P,然后给出两个下标i,j,当j-i>=k,且|Pj-Pi|=1的时候,两个元素可以交换,问达到给定排列的字典序最小的排列。
考虑一个排列Q,Q[P[i]]=i,那么以上条件就可以转换成当Qj-Qi>=k,且相邻的时候,两个元素可以交换。这样会发现当Oj-Qi<k的时候,这两个元素的相对位置是固定的,问题转换为一个图,当Qj-Qi<k的时候,Qj到Qi有一条边,然后求这个边的拓扑序列最小。
求图的拓扑序列那个部分可以用优先队列优化,问题在于建边,对于一个元素来说,我们希望找到它周围最近的符合要求的元素,来建边,用线段树来搞,在符合条件的值上是其位置的值,具体看代码。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 #include <fstream> #include <iostream> #include <functional> #include <algorithm> #include <cstring> #include <vector> #include <string> #include <cstdio> #include <cmath> #include <queue> #include <stack> #include <deque> #include <ctime> #include <list> #include <set> #include <map> using namespace std; typedef long long ll;#define eps 1e-10 #define LL_INF 0x33ffffffffffffff #define INF 0x3f3f3f3f #define mem(a, b) memset(a, b, sizeof(a)) #define sa(n) scanf("%d" , &(n)) #define mp make_pair #define ff first #define ss second #define pb push_back const int maxn = 500005 ;const ll mod = 998244353 ;const double PI = acos (-1.0 ); struct no { int le; int ri; int max_v; }node[4 * maxn]; void build (int root, int le, int ri, int v) if (le == ri) { node[root].le = le; node[root].ri = ri; node[root].max_v = v; return ; } int mid = (le + ri) >> 1 ; build (root << 1 , le, mid, v); build ((root << 1 ) | 1 , mid + 1 , ri, v); node[root].le = le; node[root].ri = ri; node[root].max_v = v; } int query (int root, int le, int ri) if (node[root].le == le&&node[root].ri == ri) { return node[root].max_v; } int mid = (node[root].le + node[root].ri) >> 1 ; if (mid >= ri) { return query (root << 1 , le, ri); } else if (mid + 1 <= le) { return query (root << 1 | 1 , le, ri); } else { return max (query (root << 1 , le, mid), query (root << 1 | 1 , mid + 1 , ri)); } } void update (int root, int k, int v) if (node[root].le == k&&node[root].ri == k) { node[root].max_v = v; return ; } int mid = (node[root].le + node[root].ri) >> 1 ; if (k <= mid) { update (root << 1 , k, v); } else { update (root << 1 | 1 , k, v); } node[root].max_v = max (node[root << 1 ].max_v, node[root << 1 | 1 ].max_v); } int n, k;int pos[maxn], out[maxn], res[maxn];vector<int >ed[maxn]; priority_queue<int >que; void solve () int i, j, m; sa (n), sa (k); for (i=1 ;i<=n;i++) { sa (m); pos[m] = i; } build (1 , 1 , n, -INF); for (i=1 ;i<=n;i++) { m = query (1 , pos[i], min (n, pos[i] + k - 1 )); if (m != -INF) { int x = m; out[pos[x]]++; ed[pos[i]].push_back (pos[x]); } update (1 , pos[i], i); } build (1 , 1 , n, -INF); for (i = n; i >= 1 ; i--) { m = query (1 , pos[i], min (n, pos[i] + k - 1 )); if (m != -INF) { int x = -m; out[pos[i]]++; ed[pos[x]].push_back (pos[i]); } update (1 , pos[i], -i); } for (i=1 ;i<=n;i++) { if (out[i] == 0 ) { que.push (i); } } for (i = n; i >= 1 ;i--) { int v = que.top (); que.pop (); res[v] = i; for (j=0 ;j<ed[v].size ();j++) { out[ed[v][j]]--; if (out[ed[v][j]] == 0 ) { que.push (ed[v][j]); } } } for (i=1 ;i<=n;i++) { printf ("%d\n" , res[i]); } } int main () solve (); return 0 ; }